「納得いかない!」「わかりやすく解説して!」今回は、そんな声の多い「モンティホール問題」の意外な答えについて3分でわかるように解説します。
出題!モンティホール問題、あなたは解けますか
有名な確率パズル「モンティホール問題」このパズル問題は、アメリカのテレビ番組「Let’s Make a Deal」に登場したもので、以下のような問題です。
①
司会者の前には3つのドアがあります。そのうち1つのドアの後ろには高価な賞品があり、残りの2つのドアの後ろにはハズレがあります。司会者だけがどのドアが当たりかを事前に知っています
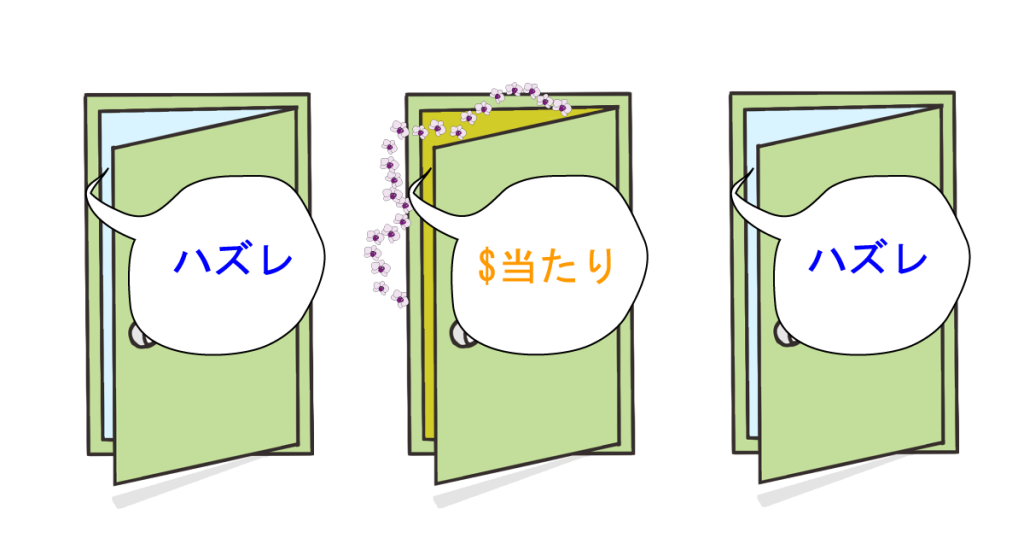
②
参加者は最初に1つのドアを選びますが、そのドアを開けることはできません。
③
次に、司会者は参加者が選んだドア以外の2つのドアのうち、ハズレがあるドアを1つ開けて見せます。
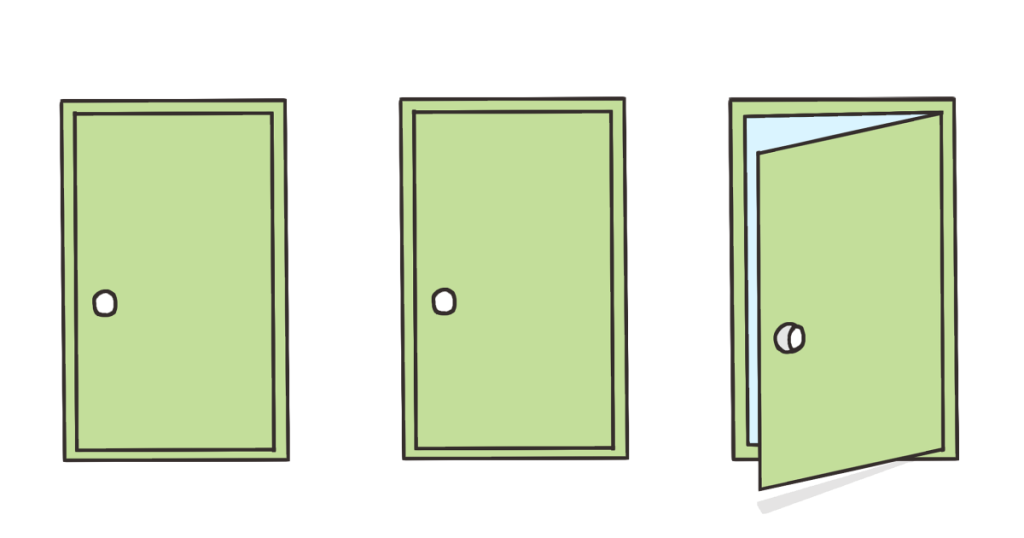
そして、司会者は参加者に「選んだドアを変えたいですか?」と聞きます。参加者は自由に答えることができます。
さて、このとき、参加者は選んだドアを変えた方がいいでしょうか?それとも変えない方がいいでしょうか?
あなたも下記3つから選んで回答してください
左の〇印をクリック → 『回答する』をクリック
意外な答えとはこれだ
選び替えた方が得です
選び替えた場合、当たりの確率は2倍になります。
選び替えなかった場合の当たりの確率は⅓、選び替えた場合の確率は⅔になります
この問題は、直感的には「どちらでも同じ」と思われるかもしれません。しかし、実は選んだドアを替えた方が賞品を当てる確率が高くなります。
次項でその理由を3分で納得させる解説をします。
これはトリックなのか
まず、最初に1つのドアを選んだとき、そのドアの後ろに賞品がある確率は1/3です。逆に外れを引いてしまい賞品が無い確率は2/3です。これは自明ですね。
ここで参加者が選んだドアには2通りのパターンがあるわけです。
- 1⃣参加者は2/3の確率のほうを引いてしまったので外れを引いている
- 2⃣参加者は1/3の確率を引き当て当たりを引いている
以上の2パターンからそれぞれ次に訪れる状態を見てみましょう
1⃣参加者は2/3の確率のほうを引いてしまったので外れを引いている場合
参加者が既に外れを引いているので司会者は必ず当たりのドアを残すことになります。
つまり参加者が選び替えたなら必ず当たりです。
この状態になるためには参加者は最初に外れを引く必要がありますがその確率は2/3です。
つまり選び替えたなら必ず当たる確率2/3に持ち込めた事になります。(しかもこのケースは当たる番です)
2⃣参加者は1/3の確率を引き当て当たりを引いている場合
参加者が既に当たりを引いているので司会者は残ったドアのどちらを開けても良い状態になります。
つまり参加者が選び替えたなら必ず外れです。
この状態になるためには参加者は最初に当たりを引く必要がありますがその確率は1/3です。
つまり選び替えたなら必ず外れる確率1/3になります。これって言い換えると
つまり選び替えたなら必ず当たる確率2/3に持ち込めた事になります。(ただしこのケースは外れる番ですが)
この問題のキモは司会者が事前に当たりドアを知っている事
結局最初にどう選んでも選び替えれば当たる確率は2/3になる事がお分かりいただけましたでしょうか。
この問題のキモは最初に参加者が選んだドアは最初から最後まで当たり確率1/3でしかないという点なのです。
何故そうなるかというと司会者は事前に当たりのドアを知っているからです。
司会者は参加者が最初にどのドアを選ぼうが必ず次に外れのドアを開ける事ができます。この事は参加者の選んだドアは全く何者をもクリアしていない事を示しています。
対して司会者すらも当たりのドアを知らない場合はどうなるのか、この場合は最初に参加者が選んだドアの当たりの確率は1/2になるのです。何故かと言うと司会者が当たりのドアを開けてしまう可能性があるため、そうならずに無事に司会者が外れを引いた時点で参加者が最初に選んだドアの確率はひとつの偶然をクリアしたのです。その偶然のクリアによって確立が1/3から1/2に引きあがったわけです。
司会者が外れのドアを開けるという行為が必然なのか偶然なのかによって参加者の選んだドアの状態が変わる・・・実に巧妙に仕組まれたパズル問題だったわけです。


コメント すみませんが海外スパムが大変多い為手動認証してます。基本、日本語のコメントは全て認証します。